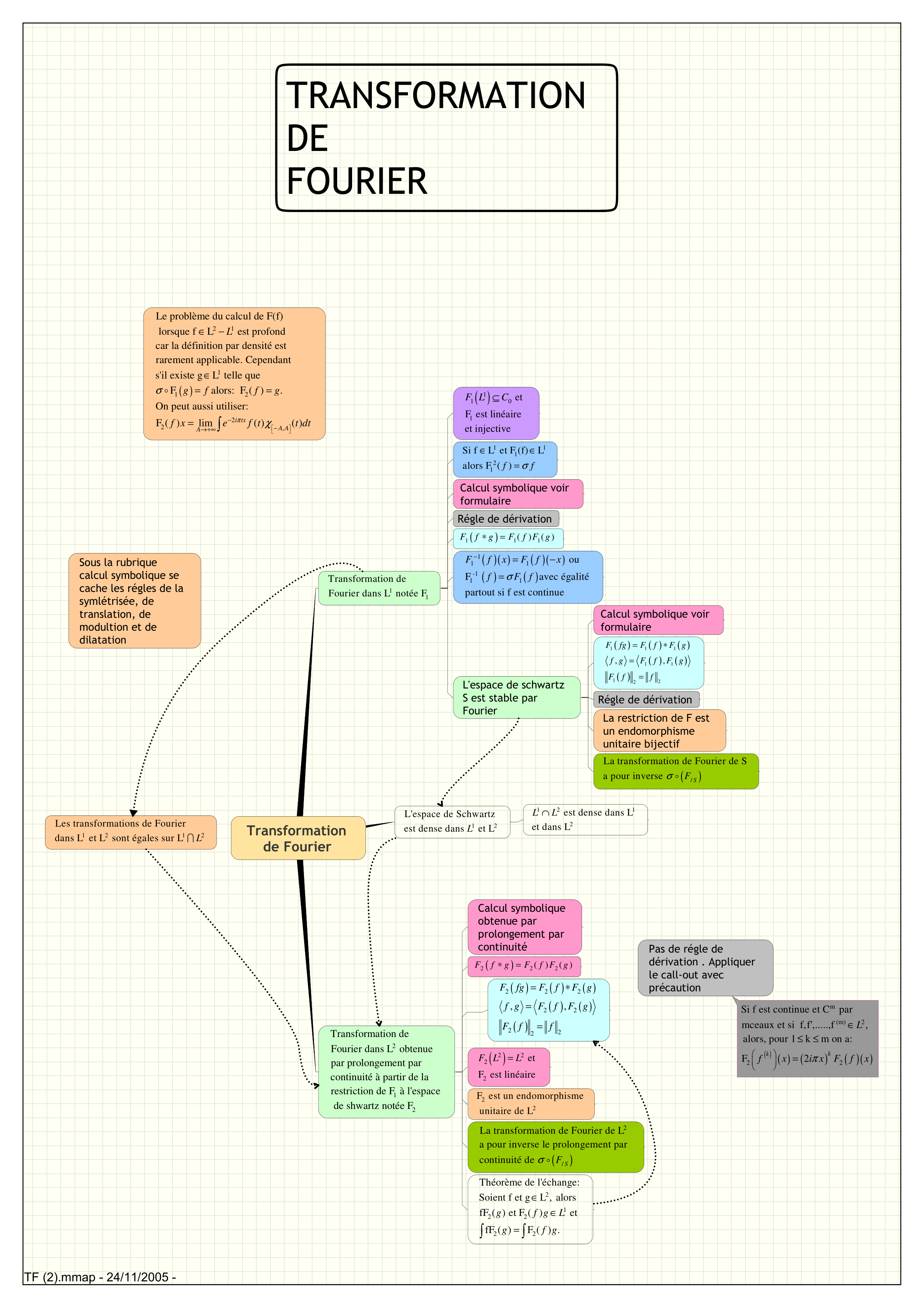
Transformation de Fourier 1 1 Transformation de Fourier dans L notée F ( ) 1 1 0 1 et F est linéaire et injective F L C ⊆ 1 1 1 2 1 Si f L et F (f) L alors F ( ) f f σ ∈ ∈ = Calcul symbolique voir formulaire Régle de dérivation ( ) 1 1 1 ( ) ( ) F f g F f F g ∗ = ( )( ) ( )( ) ( ) ( ) 1 1 1 -1 1 1 ou F avec égalité partout si f est continue F f x F f x f F f σ − = − = L'espace de schwartz S est stable par Fourier Calcul symbolique voir formulaire ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 2 2 , , F fg F f F g f g F f F g F f f = ∗ = = Régle de dérivation La restriction de F est un endomorphisme unitaire bijectif ( ) / La transformation de Fourier de S a pour inverse S F σ � 1 2 L'espace de Schwartz est dense dans et L L 1 2 1 2 est dense dans L et dans L L L ∩ 2 1 2 Transformation de Fourier dans L obtenue par prolongement par continuité à partir de la restriction de F à l'espace de shwartz notée F Calcul symbolique obtenue par prolongement par continuité ( ) 2 2 2 ( ) ( ) F f g F f F g ∗ = ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 2 , , F fg F f F g f g F f F g F f f = ∗ = = ( ) 2 2 2 2 et F est linéaire F L L = 2 2 F est un endomorphisme unitaire de L ( ) 2 / La transformation de Fourier de L a pour inverse le prolongement par continuité de S F σ � 2 1 2 2 2 2 Théorème de l'échange: Soient f et g L , alors fF ( ) et F ( ) et fF ( ) F ( ) . g f g L g f g ∈ ∈ = ∫ ∫ 1 2 1 2 Les transformations de Fourier dans L et L sont égales sur L L ∩ ( ) 2 1 1 1 2 2 Le problème du calcul de F(f) lorsque f L est profond car la définition par densité est rarement applicable. Cependant s'il existe g L telle que F alors: F ( ) . On peut aussi utiliser: F ( L g f f g f σ ∈ − ∈ = = � 2 , ) lim ( ) ( ) i tx A A A x e f t t dt π χ    − − →+∞ = ∫ Sous la rubrique calcul symbolique se cache les régles de la symlétrisée, de translation, de modultion et de dilatation TRANSFORMATION DE FOURIER Pas de régle de dérivation . Appliquer le call-out avec précaution ( ) ( ) ( ) ( )( ) m (m) 2 2 2 Si f est continue et C par mceaux et si f,f',.....,f , alors, pour 1 k m on a: F 2 k k L f x i x F f x π       ∈ ≤ ≤ = TF (2).mmap - 24/11/2005 -