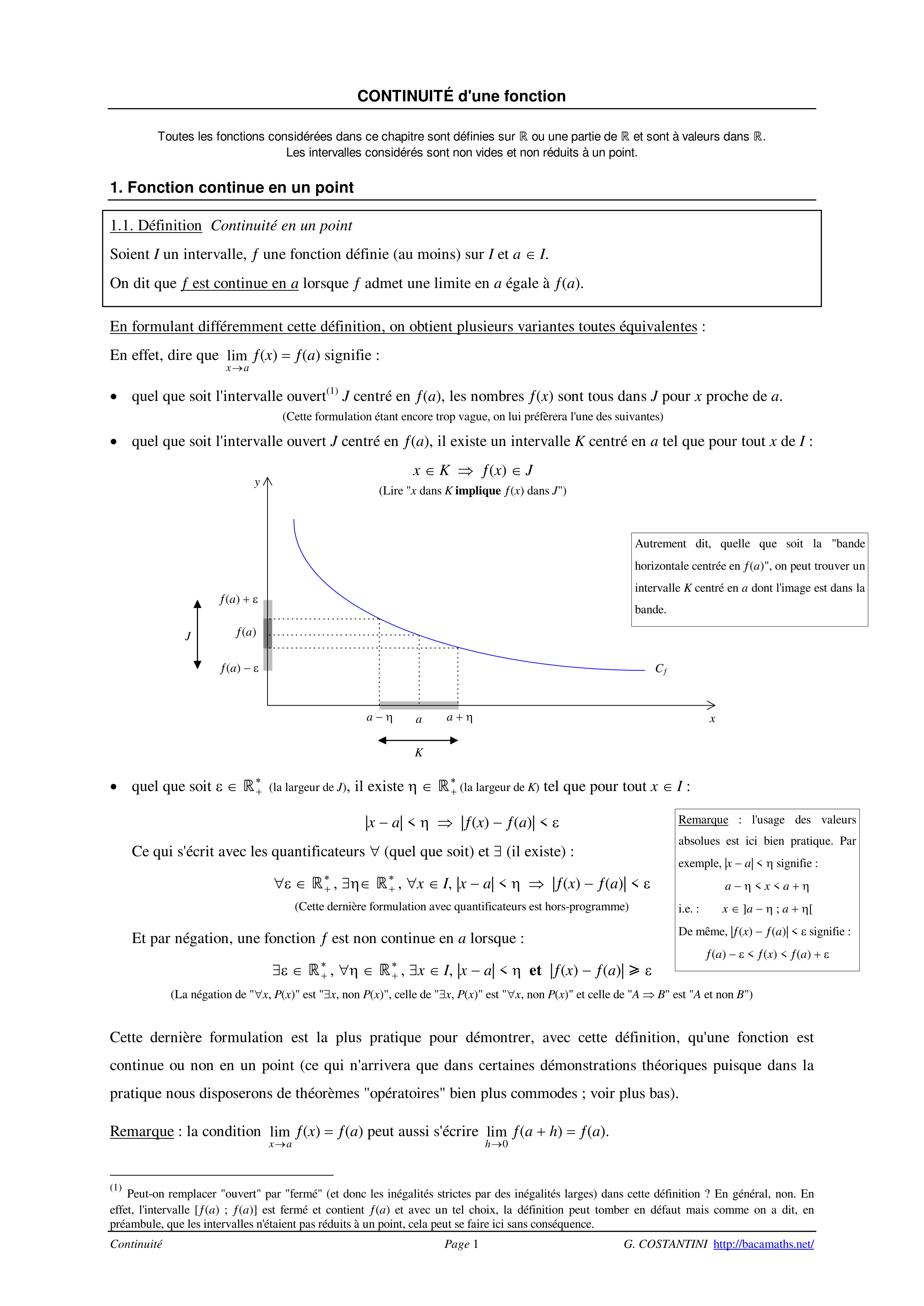
Continuité Page 1 G. COSTANTINI http://bacamaths.net/ CONTINUITÉ d'une fonction Toutes les fonctions considérées dans ce chapitre sont définies sur  ou une partie de  et sont à valeurs dans . Les intervalles considérés sont non vides et non réduits à un point. 1. Fonction continue en un point 1.1. Définition Continuité en un point Soient I un intervalle, ƒ une fonction définie (au moins) sur I et a ∈ I. On dit que ƒ est continue en a lorsque ƒ admet une limite en a égale à ƒ(a). En formulant différemment cette définition, on obtient plusieurs variantes toutes équivalentes : En effet, dire que lim x a → ƒ(x) = ƒ(a) signifie : • quel que soit l'intervalle ouvert(1) J centré en ƒ(a), les nombres ƒ(x) sont tous dans J pour x proche de a. (Cette formulation étant encore trop vague, on lui préfèrera l'une des suivantes) • quel que soit l'intervalle ouvert J centré en ƒ(a), il existe un intervalle K centré en a tel que pour tout x de I : x ∈ K ⇒ ƒ(x) ∈ J (Lire x dans K implique ƒ(x) dans J) • quel que soit ε ∈ + ∗ (la largeur de J), il existe η ∈ + ∗ (la largeur de K) tel que pour tout x ∈ I : ;;;x − a;;; < η ⇒ ;;;ƒ(x) − ƒ(a);;; < ε Ce qui s'écrit avec les quantificateurs ∀ (quel que soit) et ∃ (il existe) : ∀ε ∈ + ∗ , ∃η∈ + ∗ , ∀x ∈ I, ;;;x − a;;; < η ⇒ ;;;ƒ(x) − ƒ(a);;; < ε (Cette dernière formulation avec quantificateurs est hors-programme) Et par négation, une fonction ƒ est non continue en a lorsque : ∃ε ∈ + ∗ , ∀η ∈ + ∗ , ∃x ∈ I, ;;;x − a;;; < η et ;;;ƒ(x) − ƒ(a);;;  ε (La négation de ∀x, P(x) est ∃x, non P(x), celle de ∃x, P(x) est ∀x, non P(x) et celle de A ⇒ B est A et non B) Cette dernière formulation est la plus pratique pour démontrer, avec cette définition, qu'une fonction est continue ou non en un point (ce qui n'arrivera que dans certaines démonstrations théoriques puisque dans la pratique nous disposerons de théorèmes opératoires bien plus commodes ; voir plus bas). Remarque : la condition lim x a → ƒ(x) = ƒ(a) peut aussi s'écrire lim h→0 ƒ(a + h) = ƒ(a). (1) Peut-on remplacer ouvert par fermé (et donc les inégalités strictes par des inégalités larges) dans cette définition ? En général, non. En effet, l'intervalle [ƒ(a) ; ƒ(a)] est fermé et contient ƒ(a) et avec un tel choix, la définition peut tomber en défaut mais comme on a dit, en préambule, que les intervalles n'étaient pas réduits à un point, cela peut se faire ici sans conséquence. y ƒ(a) + ε ƒ(a) ƒ(a) − ε Cƒ x a − η a + η J a K Remarque : l'usage des valeurs absolues est ici bien pratique. Par exemple, ;;;x − a;;; < η signifie : a − η < x < a + η i.e. : x ∈ ]a − η ; a + η[ De même, ;;;ƒ(x) − ƒ(a);;; < ε signifie : ƒ(a) − ε < ƒ(x) < ƒ(a) + ε Autrement dit, quelle que soit la bande horizontale centrée en ƒ(a), on peut trouver un intervalle K centré en a dont l'image est dans la bande.