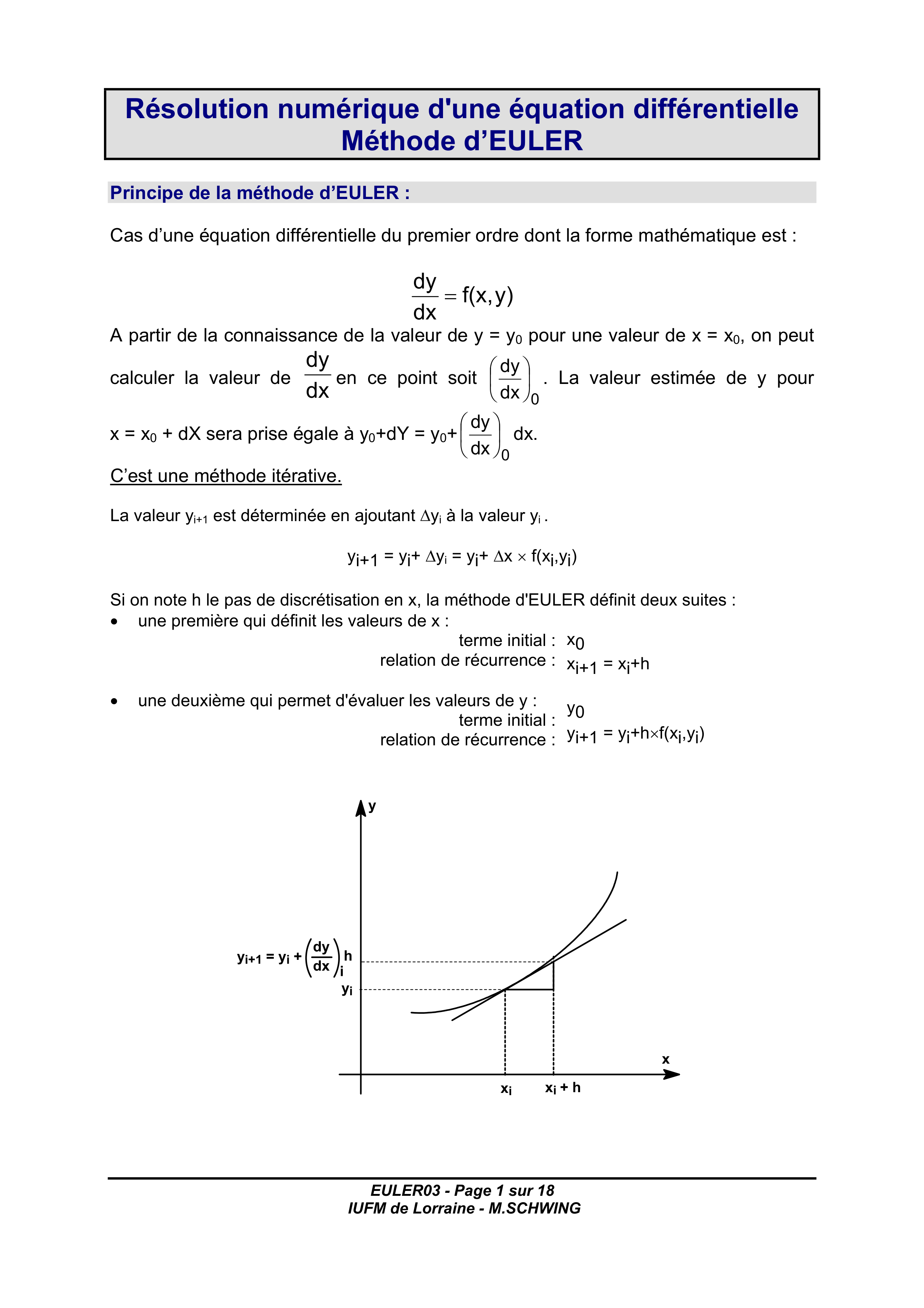
EULER03 - Page 1 sur 18 IUFM de Lorraine - M.SCHWING Résolution numérique d'une équation différentielle Méthode d’EULER Principe de la méthode d’EULER : Cas d’une équation différentielle du premier ordre dont la forme mathématique est : y) f(x, dx dy = A partir de la connaissance de la valeur de y = y0 pour une valeur de x = x0, on peut calculer la valeur de dx dy en ce point soit 0 dx dy       . La valeur estimée de y pour x = x0 + dX sera prise égale à y0+dY = y0+ 0 dx dy       dx. C’est une méthode itérative. La valeur yi+1 est déterminée en ajoutant ∆yi à la valeur yi . yi+1 = yi+ ∆yi = yi+ ∆x × f(xi,yi) Si on note h le pas de discrétisation en x, la méthode d'EULER définit deux suites : • une première qui définit les valeurs de x : terme initial : relation de récurrence : • une deuxième qui permet d'évaluer les valeurs de y : terme initial : relation de récurrence : x0 xi+1 = xi+h y0 yi+1 = yi+h×f(xi,yi) ���� ���� ������ ������ yi yi+1 = yi + dy dx i h xi xi + h y x